The most basic concept in all of chemistry is the chemical bond. The chemical bond is essentially the sharing of electrons between two atoms, a sharing which holds or bonds the atoms together. In order to understand the chemical bond, atoms and electrons must first be understood.
Table of contents:
Electron orbitals
Atoms have three components: protons, neutrons, and electrons. Protons have a positive charge of +1, neutrons have 0 charge, and electrons have a negative charge of -1. The protons and neutrons occupy the center of the atom as a piece of solid matter called the nucleus. The electrons exist in "orbitals" surrounding the nucleus. In the olden times, it was believed that the electrons orbited the nucleus in the same way that planets orbit the sun. This is not exactly true, but it explains the origin of the term orbital to describe the location of the electron.
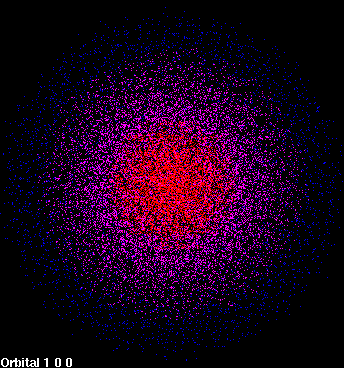
In reality, it is impossible to tell the precise trajectory of an electron in the way that the path of a planet can be followed. The best that can be achieved is to describe the probability of locating the electron in a region of space. The distribution of this probability over space is called an orbital. Let us treat the simplest case, in which the nucleus is surrounded by just one electron (for example, the hydrogen atom). In this case, the probability of finding an electron in its lowest energy, or most stable, state is distributed in a spherically symmetric way around the nucleus. The probability of finding the electron is highest at the nucleus and decreases as the distance from the nucleus increases (Figure 1).
 |
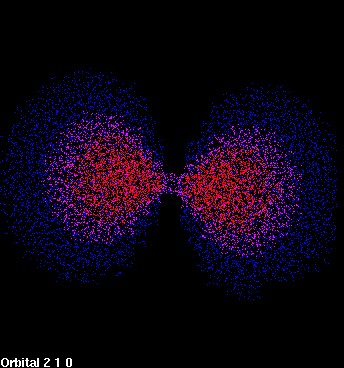 |
| Figure 1: 1s orbital | Figure 2: 2p orbital |
| The density of dots in a region represents to the probability of locating the electron there. | |
This lowest energy, spherically symmetric orbital is called the 1s orbital. As stated, in this orbital, the highest probability of finding the electron at a point in space occurs at the nucleus. Such a location may seem counterintuitive, since the electron is known to generally be located some distance from the nucleus, not directly at it. How can this apparent contradiction be explained?
Although the probability of finding the electron at a point is greatest at the nucleus, the volume of space occupied by the nucleus is extremely small compared to the rest of the atom. The probability of finding the electron at a point decreases farther from the nucleus, but the volume in which it can be found becomes much, much larger. So the electron is more likely to be found some distance from the nucleus. It is the product of the volume in which the electron can be found and the probability of finding it that gives the probability of finding the electron as a function of distance from the nucleus. The radial distribution function, which is a product of the probability and the volume element, gives the probability of finding the electron in a spherical shell some distance r from the nucleus (Figure 4). It is clear that the electron is most likely to be found in a shell some distance from the nucleus rather than directly at the nucleus. In fact, since the volume element is almost zero directly at the nucleus, the electron is very unlikely to be found there.
The 1s orbital is the lowest energy orbital that an electron can occupy, but several higher energy orbitals are significant in organic chemistry. The next lowest energy orbital that an electron can occupy is the 2s orbital, which looks much like the 1s orbital except that the electron is more likely to be found farther from the nucleus. The third lowest energy orbital is called the 2p orbital. The major and highly important difference between a p orbital and an s orbital is that the p orbital is not spherically symmetric (Figure 2). Instead, the p orbital is oriented along a specific axis in space. There are three p orbitals, oriented along the x, y, and z axes (Figure 3).
So far, our discussion of orbitals has been mathematically exact. The images of s and p orbitals depict the actual distribution over space of the probability of finding an electron in atoms with one electron. However, after a second electron is added, the problem cannot be solved exactly due to the electron-electron repulsion. Instead, approximations have to be made. Fortunately, using the exact orbitals of the one-electron atom as a basis for the orbitals in many-electron atoms is an excellent approximation. For example, in carbon, the energy of the electron is correct to within 1% using this approximation.1 Thus, orbitals in many-electron atoms look essentially like the one-electron atom orbitals that have already been described.
 |
 |
 |
| 2px orbital | 2py orbital | 2pz orbital |
| Figure 3: The three 2p orbitals | ||
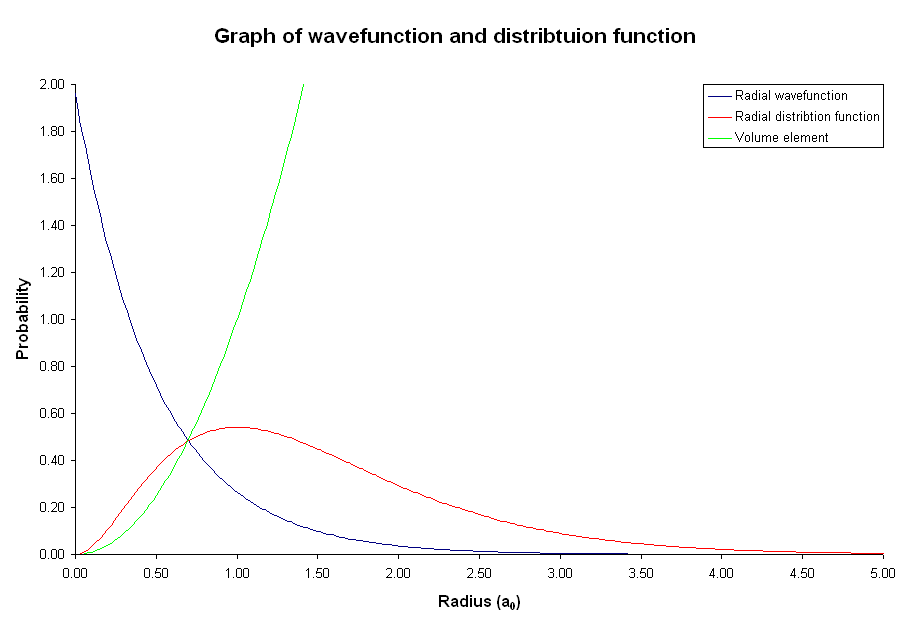
Figure 4: Graph of probability density, radial distribution function, and volume as a function of radius for the 1s electron
Bonding in carbon
We have stated that a chemical bond is essentially the sharing of electrons between two atoms. Since electrons are negatively charged and exert an attractive force on nuclei, they serve to hold the atoms together if they are located between two nuclei. How does this notion of a chemical bond relate to orbitals describing electron density? When two atoms approach each other, their atomic orbitals overlap. The overlapped atomic orbitals can add together to form molecular orbitals. This procedure is called the linear combination of atomic orbitals (LCAO). The area of greatest overlap between the original atomic orbitals represents the chemical bond that is formed between them. Since the sharing of electrons is the basis of the chemical bond, the molecular orbitals formed represent chemical bonds.
Let us take a simple example, hydrogen. We can imagine two 1s orbitals gradually coming closer and closer together until there is a good deal of overlap between them (Figure 5). At this point, the area in space of greatest electron density will be between the two nuclei, which themselves were at the center of the original atomic orbitals. This electron density, now part of a new molecular orbital, represents the chemical bond. When, as below, the area of greatest overlap occurs directly between the two nuclei on internuclear axis or axis containing the nuclei of both atoms, the bond is called a sigma bond or σ bond.
There are two final points to consider when atomic orbitals combine. First, more than one atomic orbital from a single atom can be used to form new molecular orbitals. For example, a 2s orbital and a 2p orbital from one atom might add together and overlap with one or more orbitals from a second atom to form new molecular orbitals. Second, parts of orbitals can possess a sign (+ or -). The s orbital has the same sign throughout, while in the p orbitals, one lobe is + and the other lobe is -. Signs do not matter with respect to electron density, but they must be taken into account when orbitals are added or subtracted. If two orbitals of the same sign are added, electron density will increase, while if two orbitals of opposite signs are added, the shared electron density will cancel out.
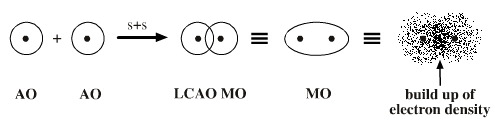
Figure 5: Two hydrogen 1s atomic orbitals overlap to form a hydrogen molecular orbital
sp3 bonds
We can now treat bonding in carbon. Carbon has six electrons. Only two electrons can occupuy an s orbital at a time. The first two electrons in carbon occupy the 1s orbital. The next two occupy the higher-energy, but similarly shaped 2s orbital. The final two electrons occupy the 2p orbitals. In carbon, the electrons in the 1s orbital are too low in energy to form bonds. Thus, electrons used to form bonds must come from the 2s and 2p orbitals. Carbon very often makes four bonds, and when it does so, these bonds are arranged so that they are as far away from each other as possible. This arrangement is referred to as tetrahedral (Figure 6).
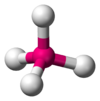
Figure 6: Tetrahedral geometry
It is clear that the individual 2s and 2p orbitals cannot form bonds in this arrangement due to their geometry. The 2s orbital is completely symmetric, while the 2p orbitals are aligned along specific axes. None of these orbitals is well-equipped to form bonds in the tetrahedral geometry alone. However, we have stated that a chemical bond doesn't have to be formed from individual atomic orbitals, but can be formed from a combination of several atomic orbitals from the same atom. For each bond that is made in the tetrahedral geometry, a part of the 2s and a part of each of the 2p orbitals will contribute, resulting in a tetrahedral arrangement. To achieve this geometry, both the 2s and all three of the 2p orbitals (2px, 2py, and 2pz) must contribute (Table 1). The new bonds that are formed are called sp3 bonds, since one s and 3 p orbitals were used to form them (Figure 7).
| Linear combination | 2s | 2px | 2py | 2pz | |||||
|---|---|---|---|---|---|---|---|---|---|
| (1/√4)(2s + 2px + 2py + 2pz) |  | + |  | + |  | + |  | = |  |
| (1/√4)(1/2s + 2px - 2py - 2pz) |  | + |  | + |  | + |  | = |  |
| (1/√4)(2s - 2px + 2py - 2pz) |  | + |  | + |  | + |  | = |  |
| (1/√4)(2s - 2px - 2py + 2pz) |  | + |  | + |  | + |  | = |  |
 |
 |
 |
 |
| Figure 7: Orbital combinations used to make sp3 bonds | |||
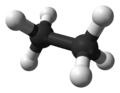 |
| Figure 8: sp3 bond between two carbon atoms |
Note that when sp3 bonds are formed, they all point in separate directions as far away from each other as possible, leading to 109.5° angles between the bonds. This is the tetrahedral geometry as shown in Figure 6. When carbon makes four sp3 bonds to hydrogen, the resulting molecule is tetrahedral in shape and looks like Figure 6. Carbon can also make a bond to another carbon atom. Two carbon atoms, both of which have sp3 bonds oriented tetrahedrally, can bond to each other if each uses one of its sp3 bonds (Figure 8).
sp2 bonds
Carbon sometimes makes just three bonds. In this case, not all of the 2p orbitals combine with the 2s orbital to form bonds. Instead, a combination of the 2s orbital and two of the 2p orbitals make three sp2 bonds, while the other p orbital does not participate in this combination and can make a fourth bond on its own (Table 2).
| Linear combination | 2s | 2px | 2py | ||||
|---|---|---|---|---|---|---|---|
| (1/√3)2s + (1/√6)2px + (1/√3)2py |  | + |  | + |  | = |  |
| (1/√3)2s + (1/√6)2px - (1/√3)2py |  | + |  | + |  | = |  |
| 2s - (2/√6)2px |  | + |  | = |  |
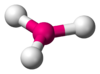 |
| Figure 9: Trigonal planar geometry |
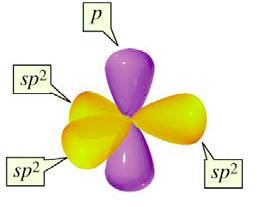 |
| Figure 10: Carbon atom with sp2 orbtials and a 2p orbital |
Like the sp3 bonds, the sp2 bonds are oriented such that they are as far away from each other as possible. This geometry is called the trigonal planar geometry (Figure 9). It is called trigonal planar since each of the bonds points to one of the vertices of a triangle, but all three bonds are located in the same plane. What about the other 2p orbital, the one which did not add to make sp2 bonds? This orbital still exists, and it is perpendicular to the plane in which the sp2 bonds form. It too is able to form bonds, and it does so independently of the sp2 bonds (Figure 10).
When two carbon atoms with sp2 orbitals form a bond to each other using their sp2 orbtials, a σ bond is formed between then. Morever, the extra p orbtials that exist above and below each carbon atom also overlap with each other. This orverlap between p orbitals leads to the formation of a second bond in addition to the σ bond formed between the sp2 orbitals. This second bond, which does not occur directly between the nuclei on the internuclear axis, but rather above and below the internuclear axis, is called a pi bond or π bond. When a σ bond and a π bond form together between two atoms, a double bond is said to have formed (Figure 11).
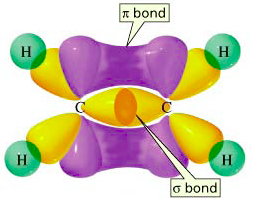
Figure 11: The molecule ethane is formed from two carbon atoms. A σ bond formed from
two sp2 orbitals
and a π bond formed from two 2p orbitals together compose a double bond.
More to come...
References
Note
This website is the result of my experience tutoring organic chemistry. It is intended to educate students in the basic principles of organic chemistry and present the material in a clear and easy to understand manner. It aims to provide greater clarity and detail and teach differently than organic chemistry textbooks.
| Previous topic: - |
1. Basic bonding concepts in orgnaic chemistry
Back to index |
Next topic: Naming hydrocarbons |